Interpretability of AI Classifiers through Logical Circuits Representation

GitHub Repo: deep-logical-circuits
Frustrated with the lack of meaningful analysis or representation of black-box deep learning models, I sought to unravel the larger black box in terms of smaller black boxes that are composed in an interpretable way. (This is the best one can hope for in general, as one would not expect AI models to always learn interpretable models).

I present a decomposition of the DNN discrete classification map into logical (AND/OR) combinations of combinations of intermediate (True/False) classifiers of the input. This representation is exact. These terms I show are very useful for model debugging and establishing trust, making particularly transparent (1) what the network learned and indeed (2) whether the network learned. We present a hierarchical decomposition.

This work was presented in a talk and poster at the 2020 Information Theory and Applications Workshop (ITA).

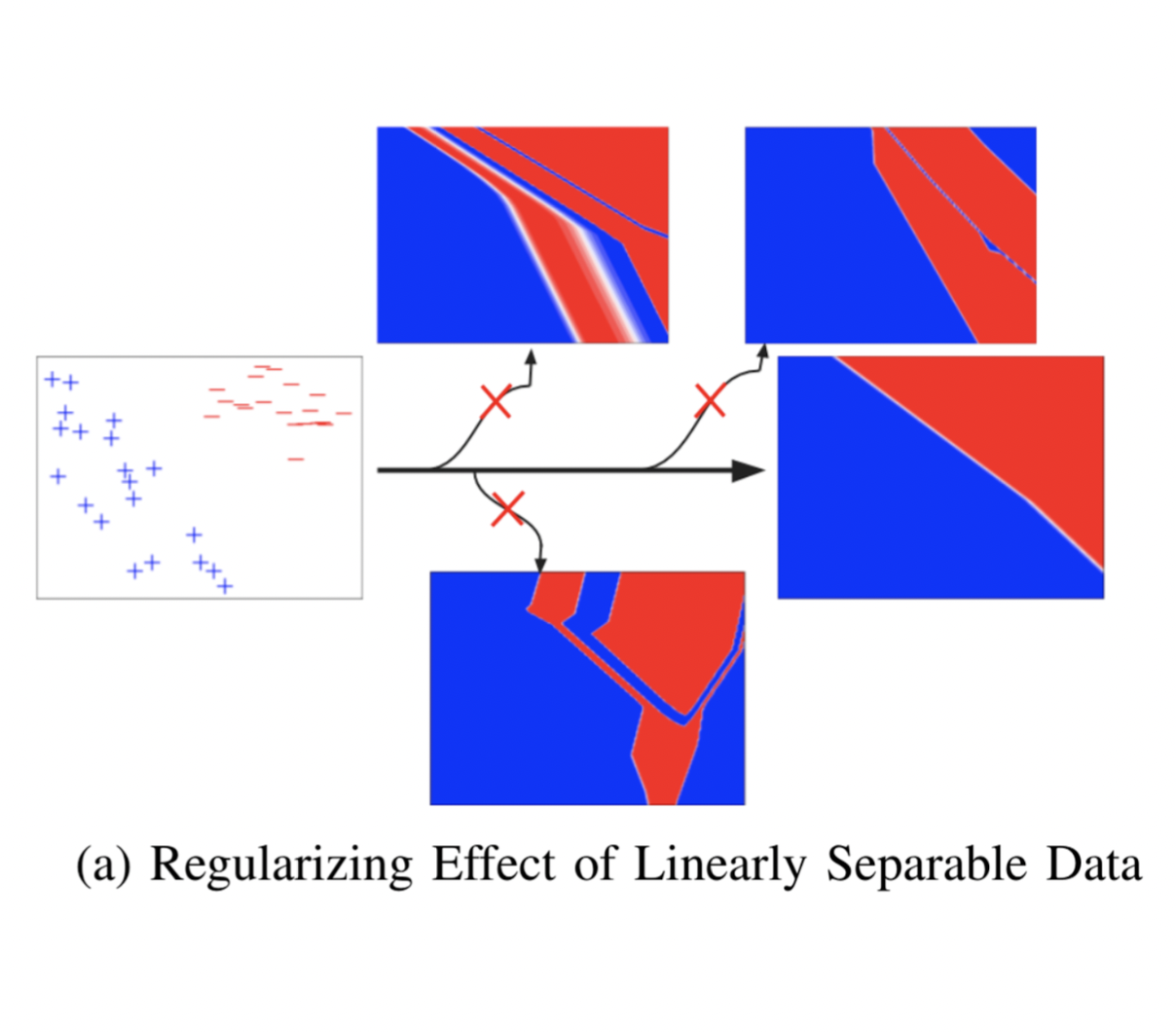
Why does simple training data produce simple models? I think this is a key question in deep learning. (Left) all 4 classifiers have the same training loss, but the nearly-linear model is chosen. First, I wanted to answer with my decomposition how one could even know from parameter values alone that a neural network model was in fact simple for higher dimensional inputs (i.e. without visualizing it!)

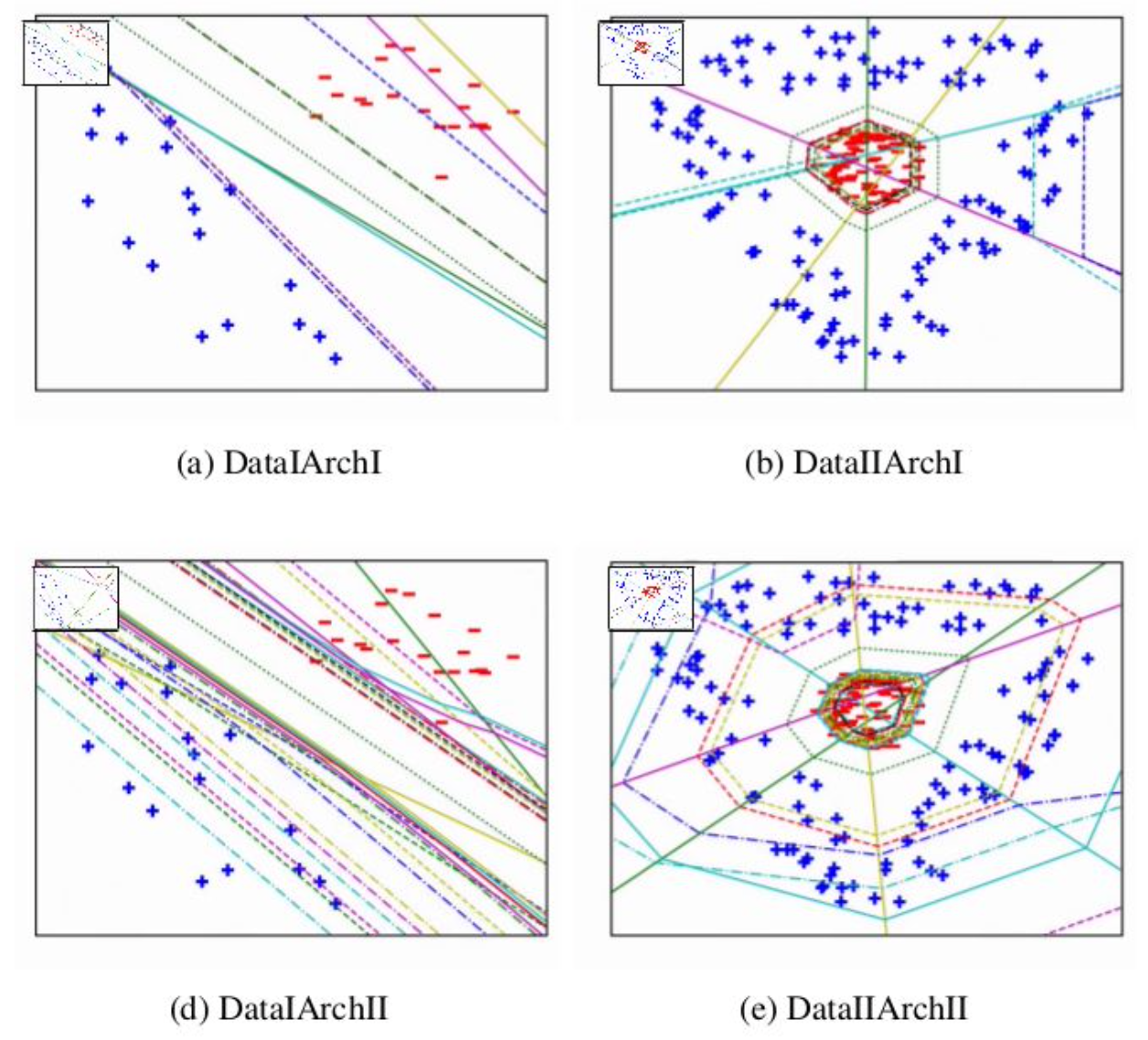
Figure (Right) shows varying neural network architexture complexity and “data complexity” of the pattern the network is trained to classify. (left col) Simple data results in the same complexity of final classifier despite using more parameters. Shown is each ReLU decision boundary of the trained network plotted (with cycling line-styles for subsequent layers) shows that the ReLU model is simple because the boundaries do not intersect. Rather they tend to become aligned on simple data–or perhaps, to the maximal extent possible given the data.

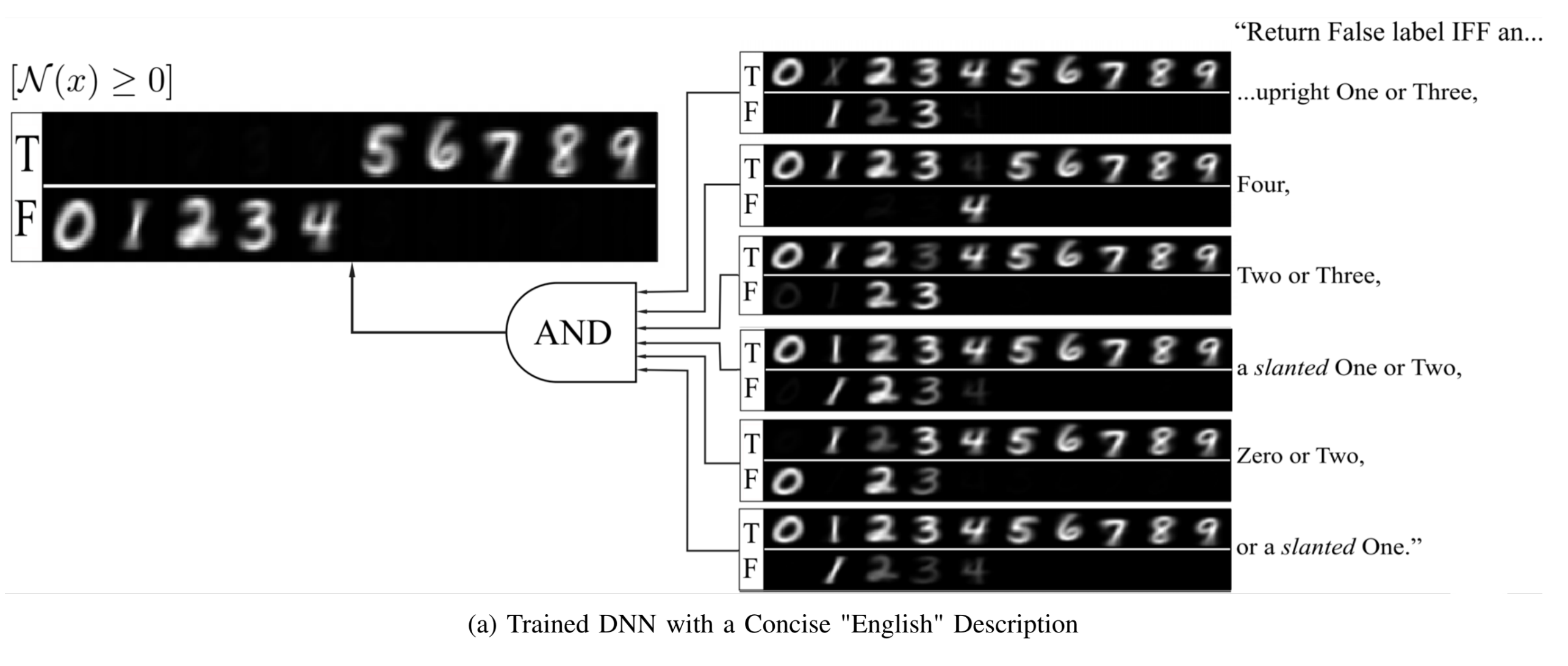
Natural Language AI Interpretation — Constituents are interpretable and specialize along semantic boundaries. We trained neural network to classify 0-4 from 5-9. Applying our representation (thm2) to this simple MNIST classifier shows an 'AND' representation of several component ("smaller black box") models, each of which has a clear responsibility in identification of particular digits or digit variations ("curly twos").

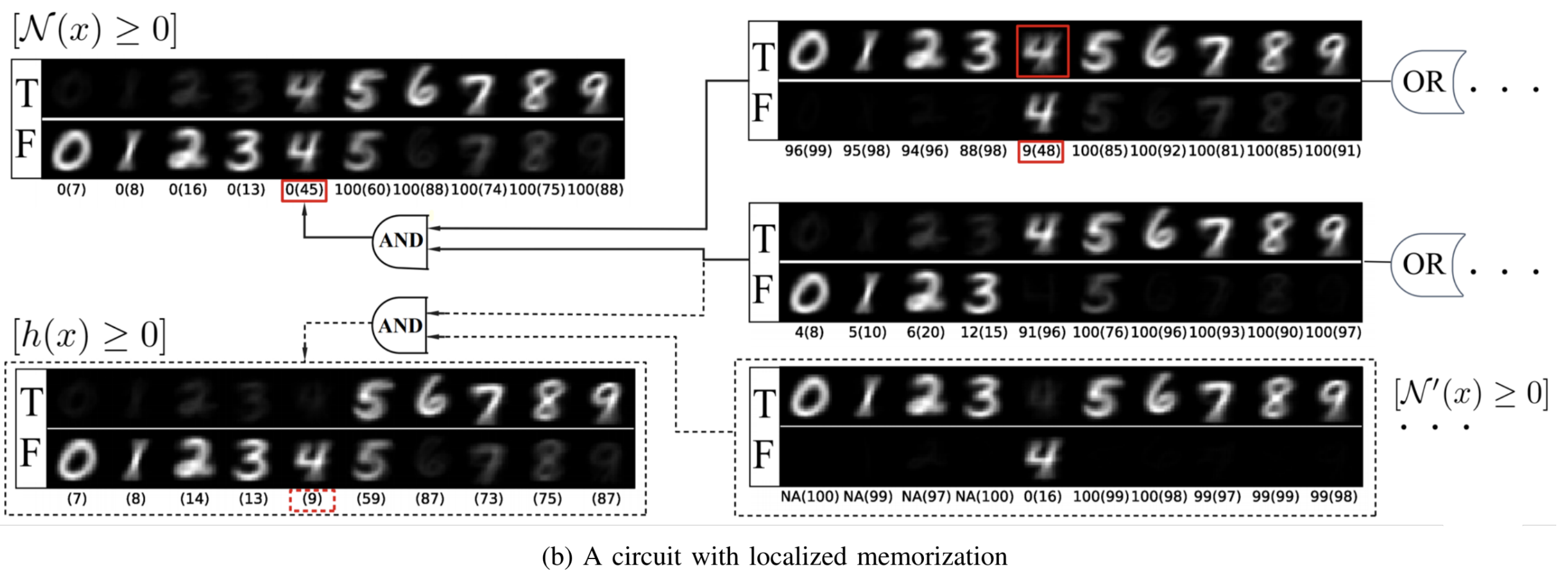
Interpretation of Overfitting — Again a classifer is trained to separate 0-4 from 5-9. For this model, it performs poorly on the 4's (by chance). The decomposition shows allows one to assign blame to a component model because the overfitting is localized (!) This can be done by simply comparing class outputs of the component models on training vs test data. In another experiment (not shown) we found that one could algebraically excize the overfitting component model from the classifier and substitute a purpose-built '4-detector' model in its place, improving the classifier's performance overall.

Public Works

Poster

Paper

Presentation

Philosophy

The approach taken in this project is in the style of the following quote:

“This is how we build knowledge. We apply our tools on simple, easy to analyze setups; we learn; and, we work our way up in complexity. . . Simple experiments — simple theorems are the building blocks that help us understand more complicated systems.”
— Ali Rahimi, NIPS2017 “Test of Time Award” talk